跳到主要内容

2-3平衡树·红黑树的前身

什么是2-3树​

  1. 为什么使用树结构
  • 从最根本的原因来看，使用树结构结束为了提升整体的效率: 插入、删除、查找(索引)，尤其是索引操作。相比于链表，一个平衡树的索引时间复杂度是O(logN)，而链表的索引时间复杂度是O(N)
    树与链表索引耗时对比: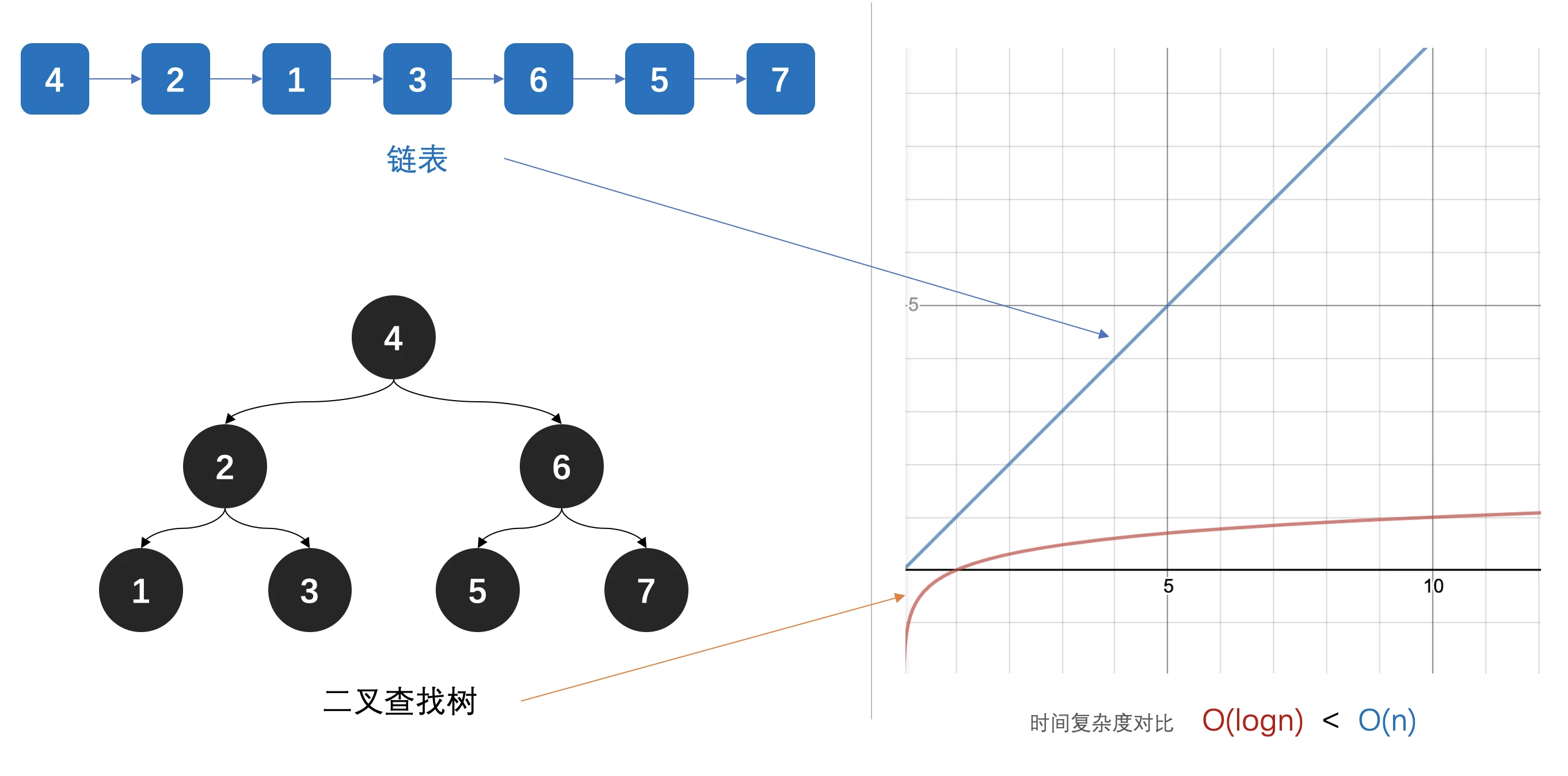
    树与链表索引耗时对比
  1. 二叉搜索树退化链表
  • 二叉搜索树退化链表
    二叉搜索树退化链表
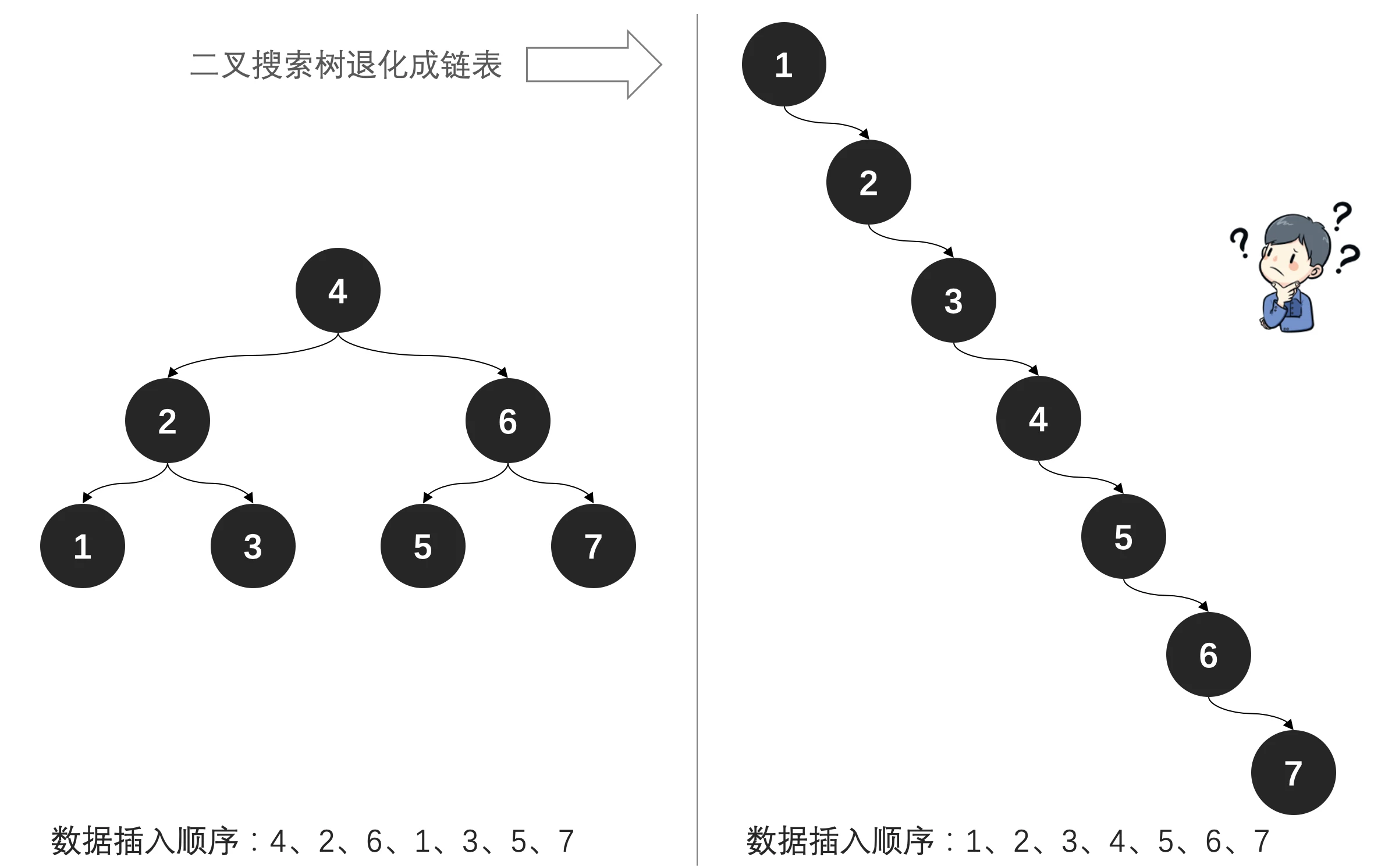
  • 二叉搜索树插入过程: 插入节点与当前树节点做比对，小于在左，大于在右
  • 随着插入顺序不同，就会出现完全不同的数据结构，可能是一颗平衡二叉树，也极有可能出现退化成链表的树
  • 当树结构退化成链表后，整个树索引的性能也随之退化成链表
  1. 2-3树解决平衡问题
  • 二叉搜索树和2-3平衡树对比
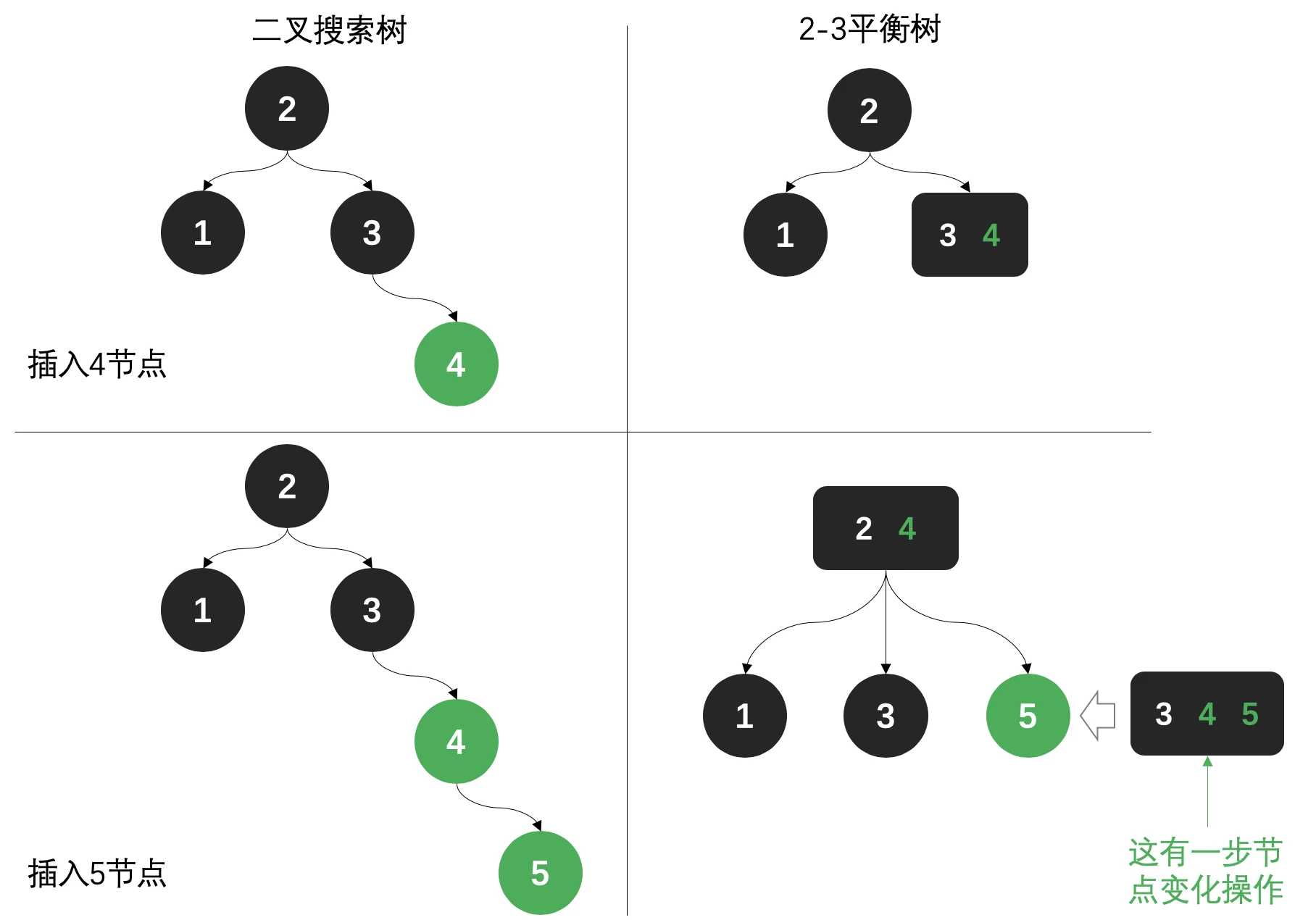
    二叉搜索树和2-3平衡树对比
  • 2-3树: 在保证树结构的基础上，允许一个节点中有两个元素，当元素数量等于3个的时候在进行调整，以保证整个二叉搜索树的平衡性

2-3树的使用​

  1. 树结构定义和特点性质
  • 2-3树的特点:
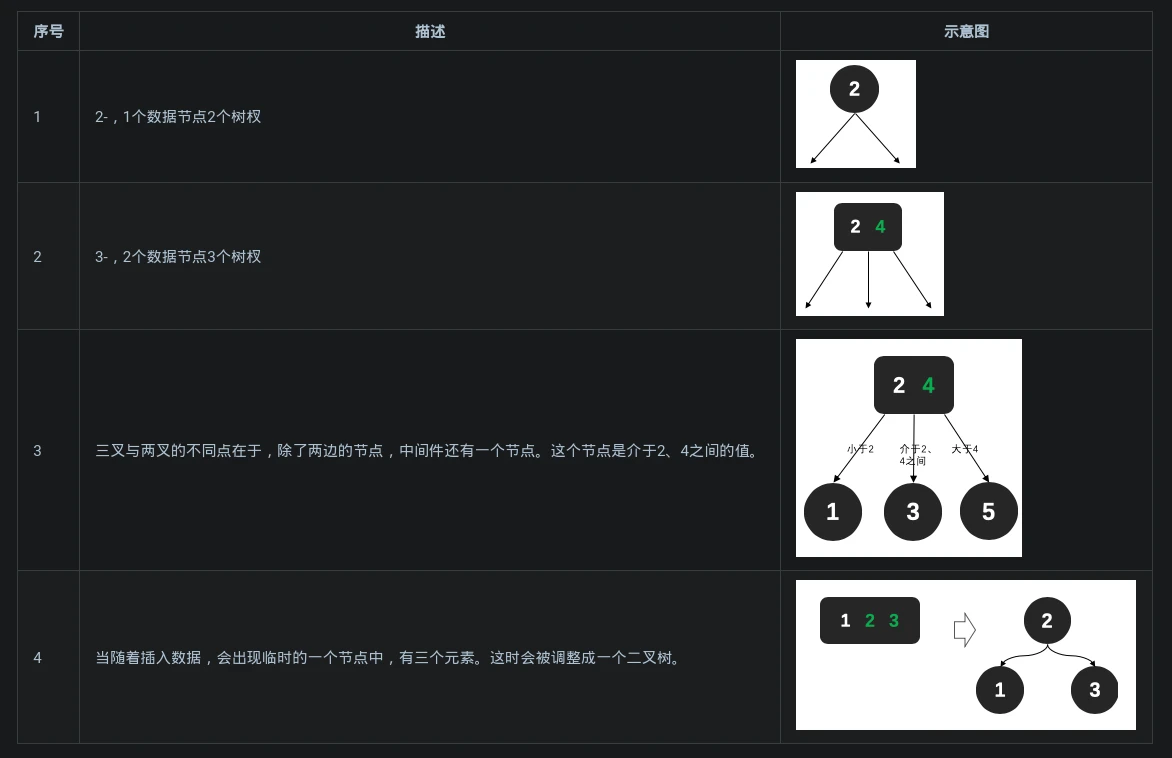
    2-3树的特点
  • 2-3树的性质:
    1. 2-3树所有的子叶节点都在同一层
    2. 1个节点可以有1-2个数据，如果有三个则需要调整树结构
    3. 1个节点1个数据时，则有两个子节点
    4. 1个节点2个数据时，则有三个子节点，且中间子节点是介于两个节点间的值

  1. 数据插入
    数据插入过程中2-3平衡树的演化
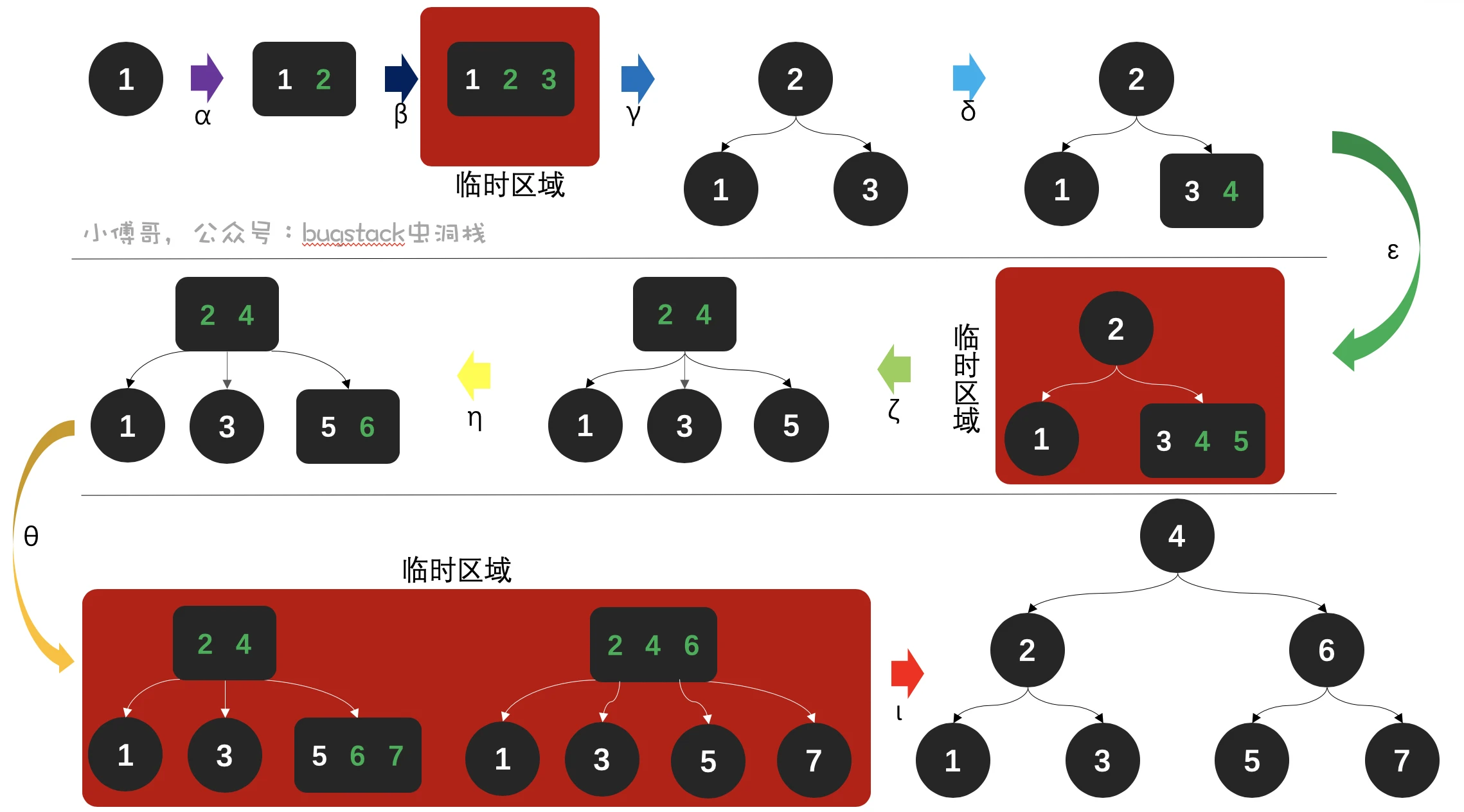
    2-3平衡树-数据插入过程中2-3平衡树的演化

    • α，向节点1插入数据2，此时为了保持平衡，不会新产生分支，只会在一个节点中存放两个节点
    • β，继续插入数据3，此时这个节点有三数据，1、2、3，是一个临时区域
    • γ，把三个数据的节点，中间节点拉起来，调整成树形结构
    • δ，继续插入数据4，为了保持树平衡，会插在节点3的右侧
    • ε，继续插入数据5，插入后3、4、5共用1个节点，当一个节点上有三个数据时候，则需要进行调整
    • ζ，中间节点4向上调整，调整后，1节点在左、3节点在中间、5节点在右
    • η ，继续插入数据6，在保持树平衡的情况下，与节点5公用
    • θ ，继续插入数据7，插入后，节点7会与当前的节点 5 6 共用。此时是一个临时存放，需要调整。初步调整后，抽出6节点，向上存放，变为2 4 6共用一个节点，这是一个临时状态，还需要继续调整
    • ι，因为根节点有三个数据2、4、6，则继续需要把中间节点上移，1、3和5、7 则分别成二叉落到节点2、节点6上

  2. 数据删除

  • 删除的两种情况:
    1. 删除了3-的节点，也就是包含两个数据元素的节点，直接删除即可，不会破坏树平衡
    2. 删除了2-的节点，此时会破坏树平衡，需要将树高缩短或者元素进行合并使树平衡恢复
  • 数据删除过程中2-3平衡树的演化
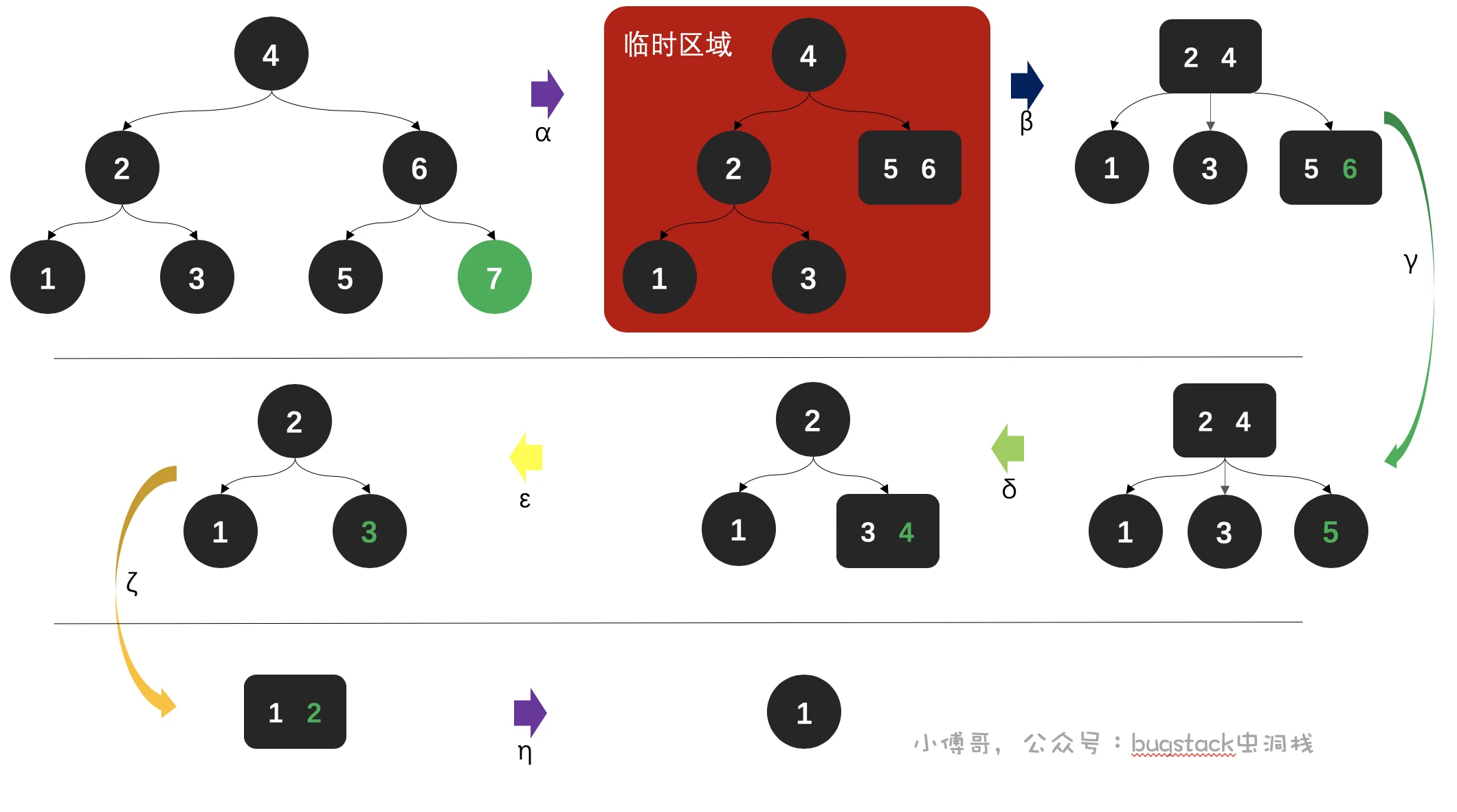
    2-3平衡树-数据删除过程中2-3平衡树的演化
    • α，删除节点7，因为节点7只有一个数据元素，删除节点5、6合并，但此时破坏了2-3树的平衡性，需要缩短树高进行调整
    • β，因为删除节点后，整个树结构不平衡，所以需要缩短树高，调整元素。节点2、4合并，节点1、3分别插入左侧和中间
    • γ，删除节点6，这个节点是3-节点(可以分出3个叉的意思)，删除后不会破坏树平衡，保持不变
    • δ，删除节点5，此时会破坏树平衡，需要把跟节点4下放，与3合并
    • ε，删除节点4，这个节点依旧是3-节点，所以不需要改变树结构
    • ζ，删除节点3，此时只有1、2节点，需要合并
    • η ，删除节点2，此时节点依旧是3-节点，所以不需要改变树结构
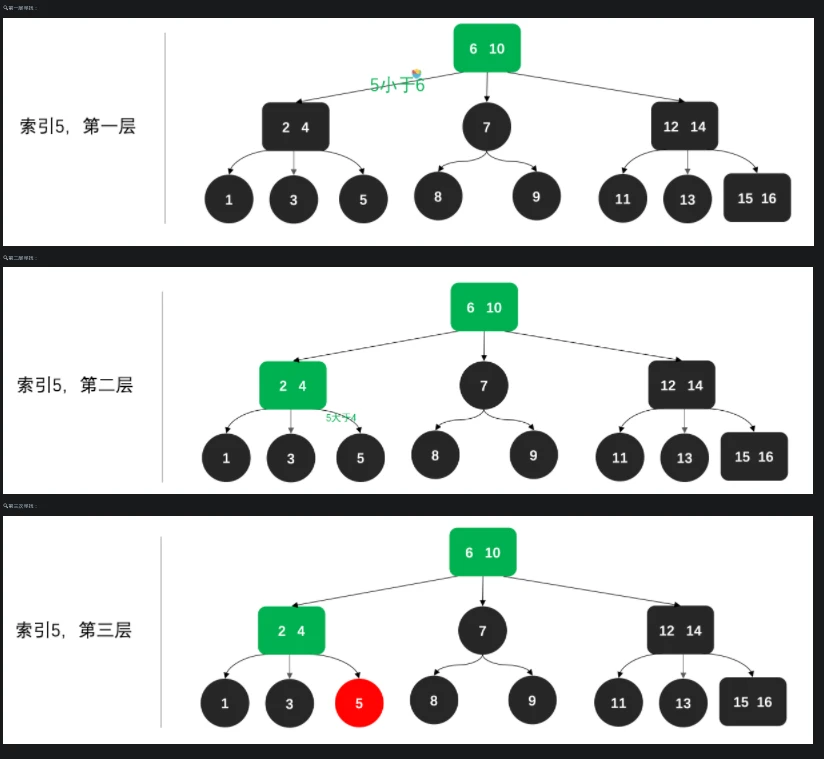
  1. 数据索引
    1. 小于当前节点值，左侧寻找
    2. 大于当前节点值，右侧寻找
    3. 一直到找到索引值，停止
      2-3平衡树-数据索引