红黑树

• 红黑树: 是一种高效的自平衡二叉查找树，最初被称为对称二叉B树，可在近似O(logN)的时间复杂度下完成插入、删除、查找等操作
• 红黑树应用: Java中的TreeMap、JDK1.8中的HashMap、C++ STL中的map

2-3树和红黑树的等价性

• 红黑树规则:
  1. 根节点是黑色
  2. 节点是红黑或者黑色
  3. 所有子叶节点都是黑色(叶子是NIL节点，默认没有画出来)
  4. 每个红色节点必须有两个黑色子节点(也同样说明一条链路上不能有链路的红色节点)
     5 黑高，从任一节点到每个叶子节点，经过的路径都包含相同数目的黑色节点

1. 为什么有了2-3树还要有红黑树

• 2-3树转红黑树由概念模型2-3-4树转换而来
• 2-3-4树具备平衡树特性，但是使用代码实现难度较高，且效率低:
  1. 2-叉、3-叉、4-叉 三种结构的节点类型互相转换复杂度较高
  2. 3-叉、4-叉，节点在数据比较上需要进行多次，不像2-叉节点，直接布尔类型比较即可判断非左即右
  3. 代码实现上对每种差异都要有而外的代码实现，规则不够标准化
     因此需要找到一种平衡关系，保持2-3树平衡和O(logN)的特性，又在代码实现上更加方便，于是就诞生了红黑树

2. 简单2-3树转红黑树

• 2-3树和2-3-4树的另一种表现形式，即更利于编码实现的方式
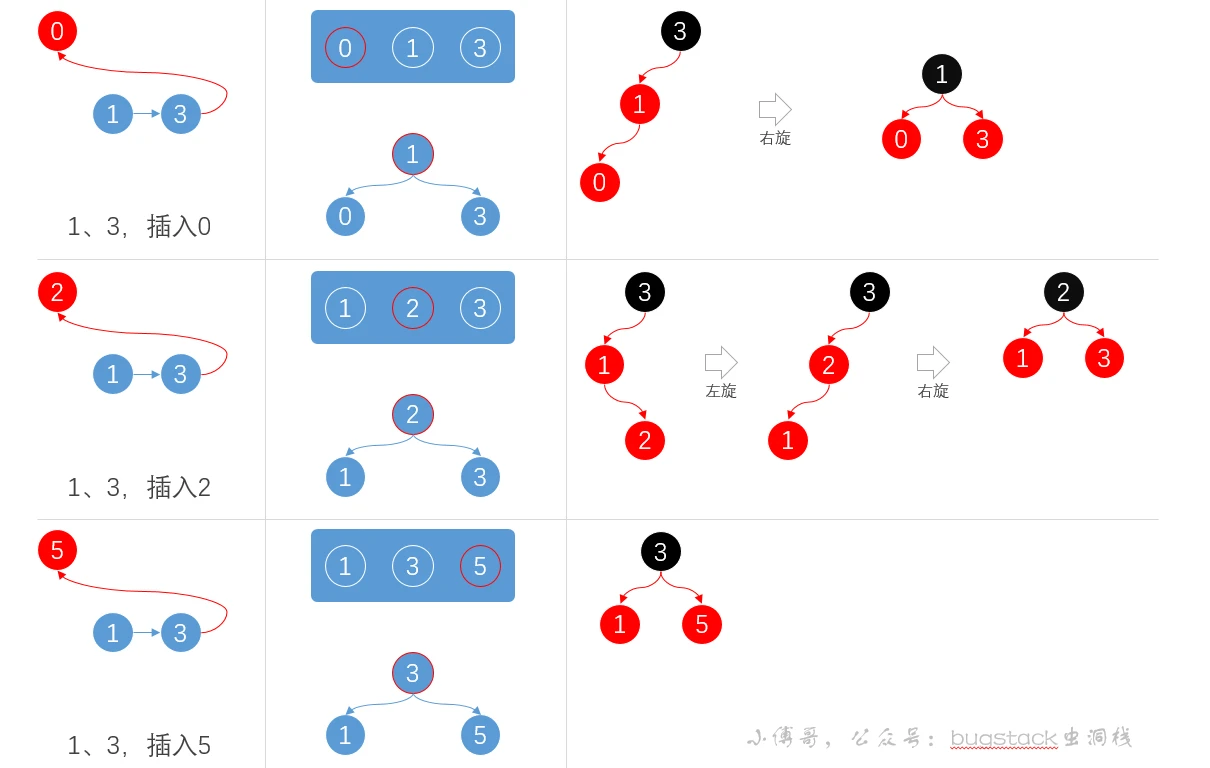
• 简单2-3树转红黑树:
  
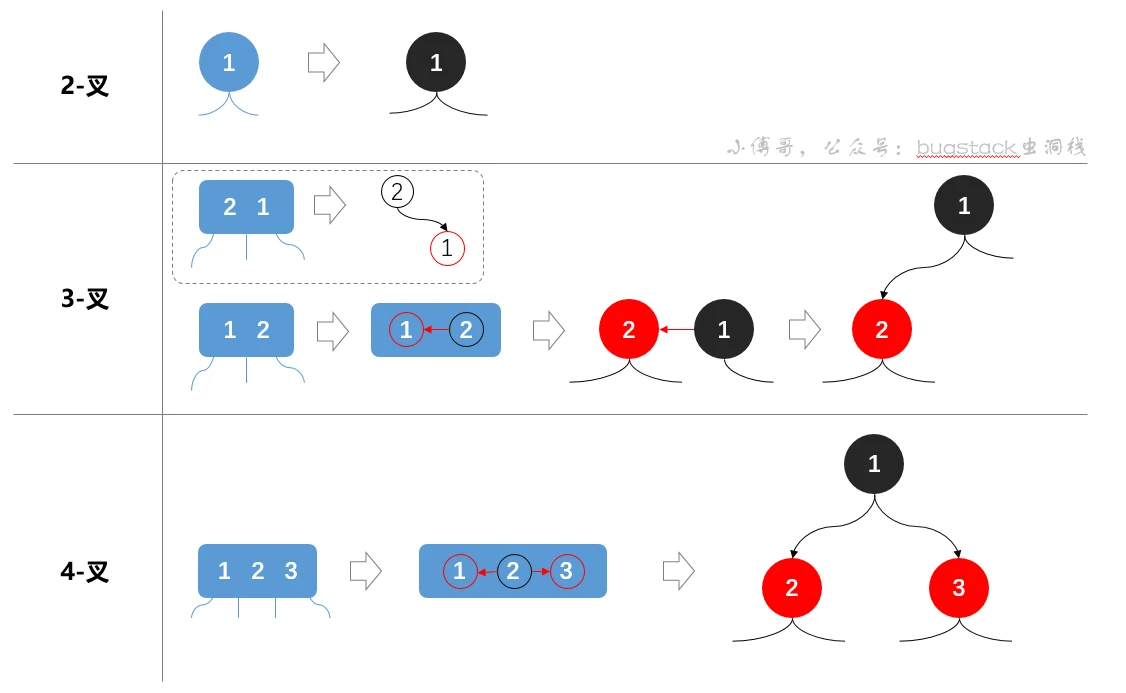
  1. 2-叉节点，原有节点转换为黑色节点
  2. 3-叉节点，包括两个元素，先用红色线将两个节点相连，然后拆分出来，最后调整高度，黑色节点在上
  3. 4-叉几点，包括三个元素，先分别用红黑线相连，然后拆分出来拉升高度，拉升过程与2-3树调整一直，只是添加了颜色
• 总结规则:
  1. 将2-3-4树用二叉树的形式表现
  2. 3-叉、4-叉节点，使用红色、黑色连线进行链接
  3. 3-叉节点有两种情况导致转换成二叉树，就有左倾和右倾

3. 复杂2-3树转红黑树
   

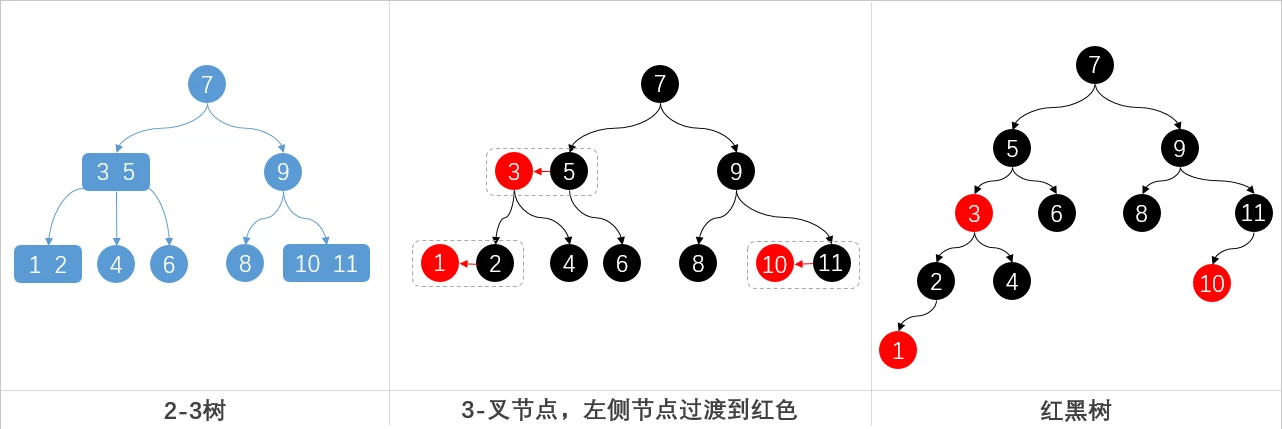
红黑树

1. 平衡操作

• 让红黑树达到平衡的操作: 染色、左右旋转，做法均由2-3树演化过来

• 左旋转:

  • 把一个向右倾斜的红节点链接(2-3树，3-叉双元素节点)转换为左链接
    
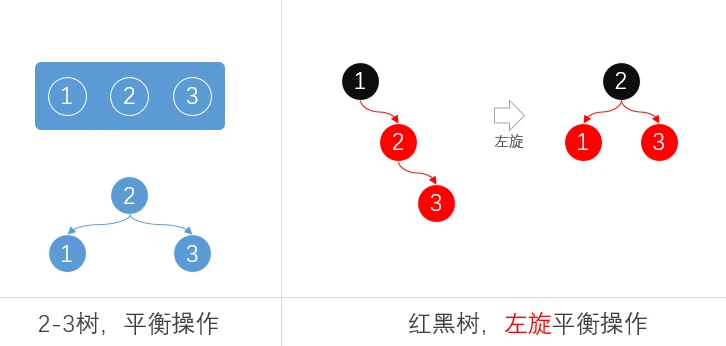
    平衡操作对比:

    • 2-3树: 所有插入的节点都会保持在一个节点上，之后通过调整节点位置保持平衡

    • 红黑树: 需要通过节点的左侧旋转，将元素2拉起来，元素1和元素3分别成为左右子节点

      红黑树的左旋，只会处理与之对应的2-3树节点进行操作，不会整体改变

• 右旋转:

  • 把一个向左倾斜的红节点链接(2-3树，3-叉双元素节点)转换为右链接
    
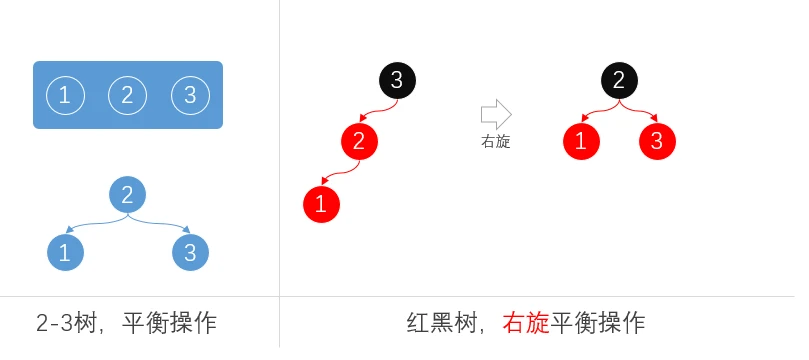
    平衡操作对比:
    • 2-3树: 所有插入的节点都会保持在一个节点上，之后通过调整节点位置保持平衡
    • 红黑树: 需要通过节点的左侧旋转，将元素2拉起来，元素1和元素3分别成为左右子节点

• 左右旋转综合运用
  

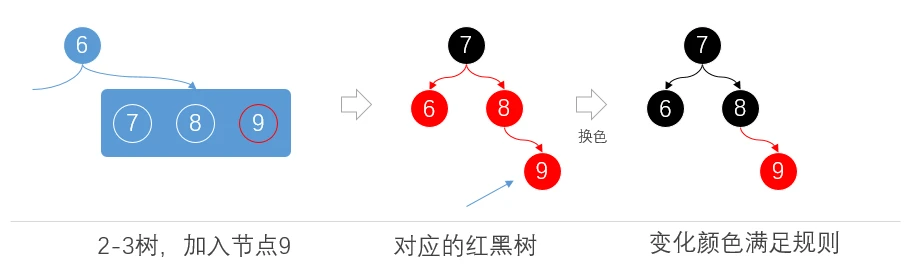
• 染色
  

• 旋转+染色综合运用
  

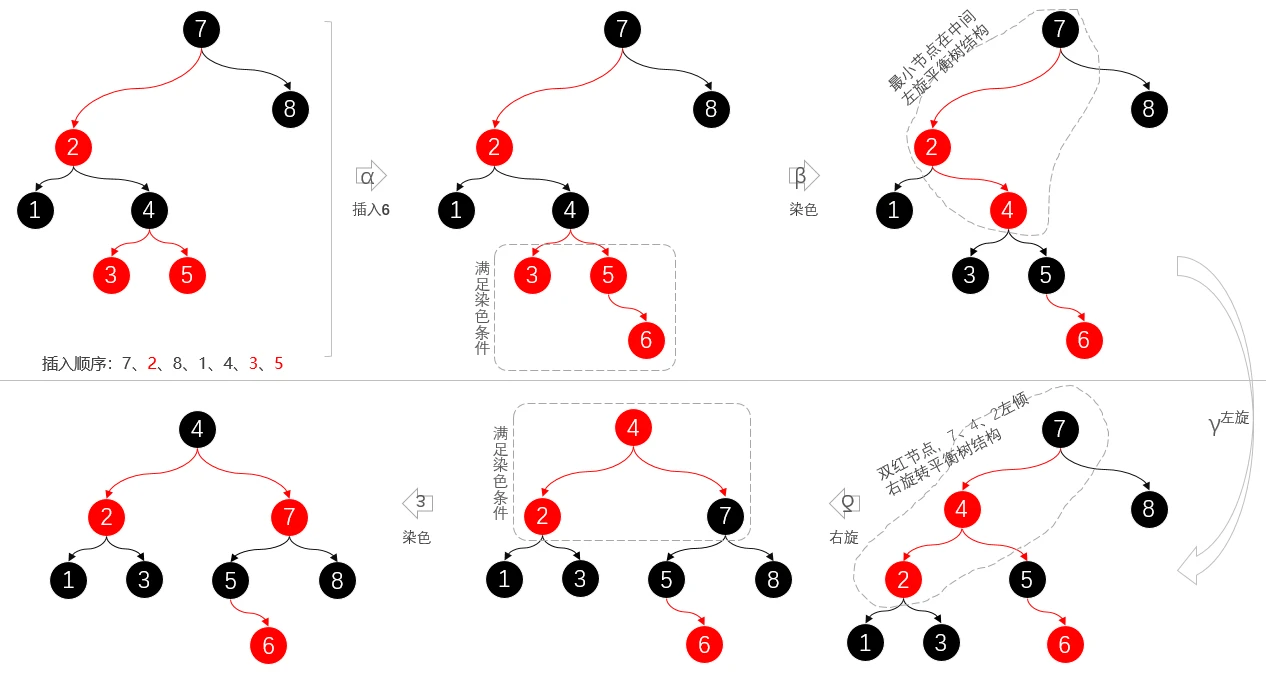
  • 首先从左侧开始，是一个按照顺序插入生产出来的红黑树，插入顺序；7、2、8、1、4、3、5
  • α，向目前红黑树插入元素6，插入后右下角有三个红色节点；3、5、6
  • β，因为右下角满足染色条件，变换后；黑色节点(3、5)、红色节点(4、6)
  • γ，之后看被红色连线链接的节点7、4、2，最小节点在中间，左旋平衡树结构
  • δ，左旋完成后，红色链接线的7、4、2为做倾顺序节点，因此需要做右旋操作
  • ε，左旋、右旋，调整完成后，又满足了染色操作。到此恢复红黑树平衡

• 删除操作
  

• 红黑树可视化: https://www.cs.usfca.edu/~galles/visualization/RedBlack.html